Beyond state-of-the-art accuracy by fostering ensemble generalization

-
Sometimes practitioners are forced to go beyond the standard methods in order to gain more accuracy with their models. If one analyzes the problem of rocketing accuracy, ensembling is a good starting point. However, the trick lies in getting enough generalization from feature space.  In this regard, ensemble generalization--do not confuse with classic or "standard" ensemble methods such as Random Forest or Gradient Boosting--is the right path to follow, however complex. The idea is to combine predictions from "base learners" to train a second stage regressor, using these predictions as metafeatures. The trick is to use a J-fold cross-validation scheme and use always the same data partitions and seed. This kind of ensemble is often called stacking--as we "stack" layers of classifiers.

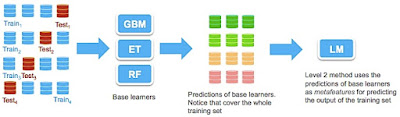
Let’s do an example: suppose that we have three base learners: GBM, ET, and RF. Then assume we have a LM as level 2 learner. First we divide the training data into J-folds, for example in 4--recall that these 4 folds are stratified and disjoint. Then we train each model using the traditional cross-validation scheme, that is train with 3 folds and predict with the remaining (works best if the predictions are in form of probabilities). These predictions are stored and will be used for training the level 2 model. Figure 1 depicts this process.

Figure 1. Ensemble generalization (also known as Stacking) training scheme. The idea is to "stack" multiple layers for generalizing further (in this example we use two layers), and use a J-fold cross-validation scheme for avoiding bias (in this example J = 4).
After training the level 2 algorithm, we can proceed with the final predictions. To do so, we train again the base learners but using the whole training set. We do this to gain up to a 20% accuracy. It is important to highlight that we’ve to assure that the random seeds are the same that in the J-fold training! Afterwards, for each test example we predict with the base learners and collect the predictions. These are the input of the level 2 algorithm, which performs the final prediction.

I used these in Kaggle a few times and I’ve to say that it makes the difference. However, I found it to be difficult to get it working and it requires a lot of processing power. There is a nice post from Triskelion explaining ensembles that gave me the inspiration to write this. 

Comments

Post a Comment

Popular posts from this blog

Data Streams and VFML

-
We live in a technological world crowded of information. Every device we can think of can give us a bunch of such data, usually in the form of a flow or stream of information in, more or less, real time . In this particular situation classical knowledge discovery mechanisms (like our loved C4.5, a decision tree developed by Quinlan) are completely unable of extract a correct model of the situation. But, what is so special with flows of data? Following the words of Gama and Rodriques: a data stream is an ordered sequence of instances that can be read only once or a small number of times using limited computing and storage capabilities. These sources of data are characterized by being open-ended, following at high speed, and generated by non-stationary distributions in dynamic environments . So, to properly handle this kind of knowledge the learning algorithm has to learn on line and process massive amounts of data increasing the challenges to be faced. Let's hold one's breath w...
Read more

Toward ensemble methods: A primer with Random Forest

-
The Kaggle-Higgs competition has attracted my attention very much lately. In this particular challenge, the goal is to generate a predictive model out of a bunch of data taken from distinct LHC’s detectors. The numbers are the following: 250000 properly labeled instances, 30 real-valued features (containing missing values), and two classes, namely background { b } and signal { s }. Also, the site provides a test set consisting of 550000 unlabeled instances. There are nearly 1300 participants while I am writing this post, and a lot of distinct methods are put to the test to win the challenge. Very interestingly, ensemble methods are all in the head of the leaderboard, and the surprise is XGBoost , a gradient boosting method that makes use of binary trees.   After checking the computational horsepower of the XGBoost algorithm by myself, I decided to take a closer look at ensemble methods. To start with, I implemented a Random Forest , an algorithm that consists of many indep...
Read more

Optimization: Simplex Algorithm

-
Imagine we have a set of computers running simulations. Those computers can be described by a group of features, for example its power consumption per hour and the total number of processes it can run per hour. From our R+D personnel, a series of programs are send to these computers so we have to perform some schedule to run the applications, but for our profit we wish to minimise the total consumption of the set of machines. Let's show some more detail: Computer 1 has a power consumption of 100 watts per hour and can run 10  high cpu-demanding processes per hour and 7 low cpu-demanding processes per hour at the same time. Computer 2 has a power consumption of 350 watts per hour and can run 60 high cpu-demanding processes per hour and 20 low cpu-demanding processes per hour at the same time. From the R+D area there are a set of at least 3125 high cpu-demanding processes and at least 710 low cpu-demanding processes to be processed. How many hours should o...
Read more